Magnifier Tesla Coil
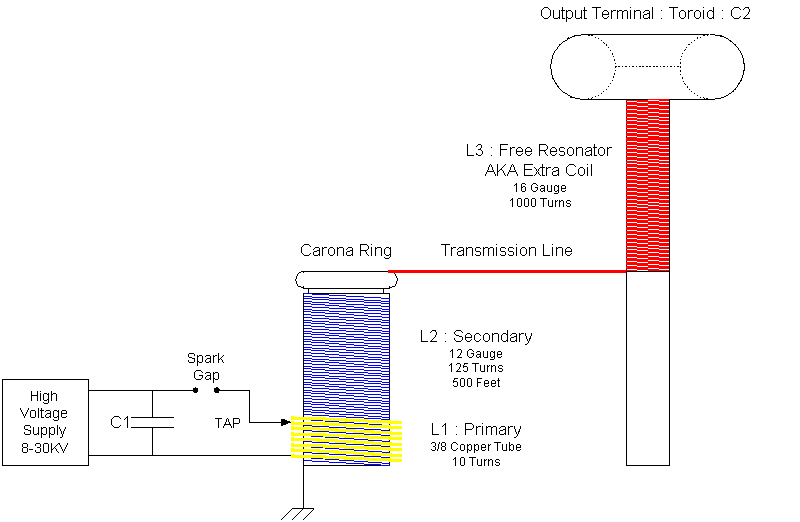
The parameters given for L1, L2, and L3 are for the magnifier I plan to build, considered a mid-size.
|
Theory In a Classic Tesla coil, the magnetic coupling between L1 and L2 is around 20% (0.2). Tesla realized this caused a lot of loss, and he abandoned the design in favor of a 3 coil system with a very high coupling (60%). Instead of a flat helical primary that has low coupling, the magnifier primary is a cylinder shape that partially encloses the secondary. Instead of a resonant transformer, L1||L2 form a standard transformer that is based on turns ratio. In fact, L1||L2 take on the role of a signal generator with a very low impedance, typically just the DC resistance of the secondary wire (1-2 Ohms). The signal generator drives the "Extra Coil", which is a free resonator. There is no mutual coupling from the free resonator to any other coil, so it can achieve higher efficiencies. Maybe. The upshot of all this is that the magnifier gets closer to the maximum efficiency possible for give input power. But this is not universally accepted by the Tesla community. In fact, many think that a well made classic TC can match the performance of the magnifier TC. The only benefit that the magnifer has is that it can achieve the high efficiency even if not well made. So, I don't know. But I'm gonna make one anyway. Check out the following for a ton of information from the expert on magnifiers. |
Some magnifier photos.

Tesla Magnifier built by Wild Bill Emery and Bert
Pool.
Primary and secondary are toward the back, on the left side of the
garage. The transmission line is a wide strip of aluminum flashing.
The coil on far left is not powered, but was built for a twin magnifier
that proved very challenging.
Photos by Steve Cole - Teslathon, NY 1995

This magnifier was built by Ed Wingate.
The primary and secondary are on the left, as is a glimpse at the distribution transformer insulators.
The extra coil has a double-toroid stack. 10-12 foot arcs!

Magnifier Project


